Things You Need to Know About Trigonometry
Trigonometry, every bit the proper noun might suggest, is all about triangles.
More specifically, trigonometry is about right-angled triangles, where one of the internal angles is 90°. Trigonometry is a system that helps us to piece of work out missing or unknown side lengths or angles in a triangle.
At that place is more most triangles on our page on Polygons should y'all need to brush up on the basics before y'all read farther hither.
Correct-Angled Triangles: A Reminder
A correct-angled triangle has a unmarried right bending. By definition, that means that all sides cannot be the same length. A typical right-angled triangle is shown below.
Of import Terms for Right-Angled Triangles

-
The right angle is indicated by the little box in the corner.
-
The other bending that we (unremarkably) know is indicated past θ (theta).
-
The side reverse the correct angle, which is the longest side, is called the hypotenuse.
-
The side contrary θ is chosen the opposite.
-
The side next to θ which is not the hypotenuse is called the adjacent.
Pythagoras' Theorem vs. Trigonometry
Pythagoras was a Greek philosopher who lived over 2500 years ago. He is credited with a number of important mathematical and scientific discoveries, arguably the nearly meaning of which has go known as Pythagoras' Theorem.
It is an important rule that applies but to right-angled triangles. Information technology says that 'the square on the hypotenuse is equal to the sum of the squares on the other 2 sides.'
That sounds rather complicated, only information technology is really quite a simple concept when we come across it in a diagram:

Pythagoras' Theorem says :
a2 + b2 = c2
So, if nosotros know the length of ii sides of a triangle and we need to calculate the third, nosotros tin can use Pythagoras' Theorem.
However, if we know just one side length and one of the internal angles, then Pythagoras is no use to usa on its own and we need to use trigonometry.
Introducing Sine, Cosine and Tangent
There are iii bones functions in trigonometry, each of which is i side of a right-angled triangle divided by another.
The three functions are:
| Name | Abridgement | Relationship to sides of the triangle |
| Sine | Sin | Sin (θ) = Opposite/hypotenuse |
| Cosine | Cos | Cos (θ) = Next/hypotenuse |
| Tangent | Tan | Tan (θ) = Opposite/adjacent |
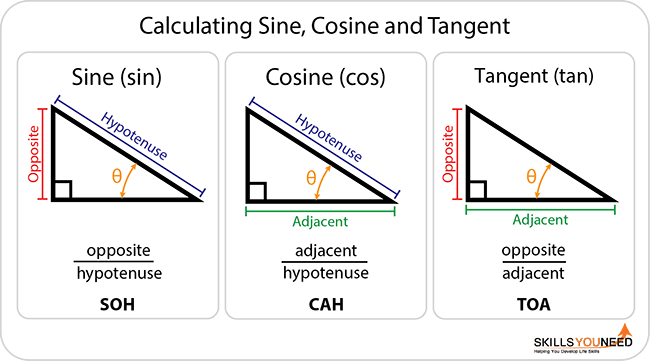
You may find it helpful to remember Sine, Cosine and Tangent equally SOH CAH TOA.
Remembering trigonometric functions can exist difficult and confusing to brainstorm with. Even SOH CAH TOA tin can be tricky. Yous could try making upwards a funny mnemonic to help you lot recall. Just keep each grouping of 3 messages in the same order.
For example, TOA SOH CAH could exist 'The Old Archaeologist Southat On His Coat And Hat'.
Peak Tip!
Because of the relationships between them, Tan θ tin as well be calculated equally:
Sin θ / Cos θ.
This means that:
- Sin θ = Cos θ × Tan θ and
- Cos θ = Sin θ / Tan θ.
Trigonometry in a Circle
For more about circles, or a quick refresher, come across our page on Circles and Curved Shapes.
When considering triangles, we are express to angles less than ninety°. However, trigonometry is equally applicative to all angles, from 0 to 360°. To understand how the trigonometric functions piece of work with angles greater than 90°, it is helpful to recall nearly triangles constructed within a circle.
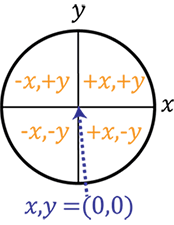
Consider a circumvolve, divided into four quadrants.
Conventionally, the middle of the circumvolve is considered as a Cartesian coordinate of (0,0). That is, the ten value is 0 and the y value is 0. For more almost this, run into our page on Cartesian coordinates.
Annihilation to the left of the centre has an ten value of less than 0, or is negative, while anything to the right has a positive value.
Similarly anything below the heart point has a y value of less than 0, or is negative and any point in the top of the circumvolve has a positive y value.

Diagram i shows what happens if we draw a radius from the centre of the circle to the right along the x centrality (we say this is in a positive direction).
We and so rotate the radius in an anticlockwise direction through an bending theta θ. This creates a right-angled triangle.
| Sin θ = | opposite (red line) |
| hypotenuse (blue line) |
| Cos θ = | adjacent (green line) |
| hypotenuse (blueish line) |
In Diagram ii , we take rotated the radius farther in an anti-clockwise direction, past the vertical (y axis) into the next quadrant. Here θ is an obtuse angle, between xc° and 180°. The reference bending blastoff α is equal to 180° − θ, and is the acute angle inside the right-angled triangle.
| Sin θ = Sin α = | opposite (cherry-red line) |
| hypotenuse (blueish line) |
Both the blue and red lines are positive, so sin θ is positive.
| Cos θ = −Cos α = | adjacent (green line) |
| hypotenuse (blue line) |
Cos θ is negative, since the greenish line is negative (it lies forth the 10 axis to the left of the origin (0,0), so is in the negative department of the 10 axis).
In Diagram iii , the radius has rotated further anticlockwise into the next quadrant then that the value of θ is between 180° and 270°. The green, cerise and blue lines all have negative values and α = θ − 180°. Sines and cosines are therefore all positive in value.
Diagram iv shows the final quadrant. The value of θ is between 270° and 360°, the green line is positive, just the ruby and blue lines are negative. Sin θ is therefore positive and Cos θ is negative. α = 360° − θ.
The Unit Circle
The 'Unit Circle' is a special example of the circle shown in the diagrams to a higher place. The Unit of measurement Circumvolve has a radius of i.
When working with a unit circle we can measure out cos, sin and tan directly:

Graphs of Sine, Cosine and Tangent
The relationship between the angle and the sin or cos can be drawn as a graph:
- y = sin (θ)
- y = cos (θ)

You tin see that when θ is 0, and so so is sine. This makes sense when you wait at the unit circle diagram to a higher place. When θ = 0, the adjacent and hypotenuse both prevarication along the positive 10 centrality and the red line that shows the value of sin θ disappears (there is no triangle).
The cosine graph is the same shape to sine, but has a value of 1 when θ = 0. Looking again at the circle to a higher place, when θ = 0, the adjacent and hypotenuse both lie along the positive ten axis and have the aforementioned value, so adjacent/hypotenuse = ane.
The cyclic nature of the sine and cosine graphs is incredibly important throughout science, nature and engineering science. Examples include electric applications (alternating current), audio and radio waves, elementary harmonic motion (such as a swinging pendulum), the trajectory of satellites, or the ascension and falling of the tide.
The amplitude of a cyclic wave blueprint is the value of the 'acme' in the graph, i.e. the distance from the x-axis to the maximum or minimum value. In the Sine and Cosine graphs above, the amplitude has a value of 1. In applications such equally sound or electric current, the aamplitude varies, depending on the volume of the sound or magnitude of the current. The amplitude of the tides also varies, depending on the position of the moon and its 'pull' on the earth.
The characteristics of the tangent graph (tan θ) are quite different. The tangent graph does not have an amplitude (wave-like characteristics) because information technology has no maximum or minimum peak values. It changes from −∞ to +∞ (negative and positive infinity) crossing through 0 every 180°:
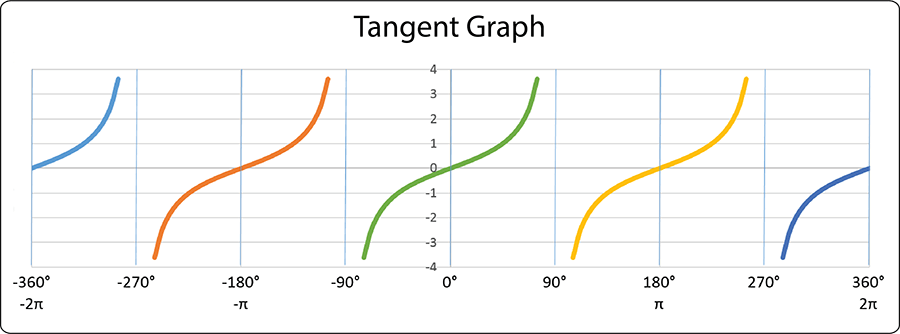
At infinity (positive or negative) information technology is said to beundefined. We tin can sympathise this graph better when we consider the equation tan θ = sin θ / cos θ. Whenever sin θ is nix, and then tan θ must also be nix. Conversely, whenever cos θ is zero, then the denominator in the equation becomes null. Annihilation divided past zero has a value of infinity, so the values of θ that have a cosine of zilch besides have a tangent of infinity on the graph. Infinity doesn't take an exact value, so the lines on the tangent graph become more and more vertical as the y centrality increases to greater and greater values. The lines go closer and closer to the vertical lines on the graph for particular values of θ, for case at 90°. Each of these vertical lines is called an asymptote.
Changed of Sine, Cosine and Tangent
You tin also work out the inverse role to sin, cos and tan, which means 1 divided past that function. They are designated as sin/cos/tan -1. This enables you lot to piece of work out the angle if you have the sin, cos or tan of information technology.
In other words:
- Sin (xc) = 1
- Sin−1 (1) = 90°
Trigonometry and Calculators
Scientific calculators take sin, cos, and tan functions, likewise as inverse functions. It's worth taking a few minutes to work out how your calculator operates, equally this could salve you hours of messing about when you need it.
Other Triangles and Trigonometry
Trigonometry also works for other triangles, only non in quite the same style. Instead there are two rules based on a triangle like this:
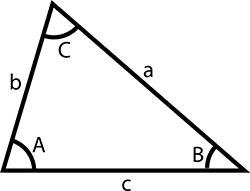
The Sine rule is:
a/sin A = b/sin B = c/sin C
The Cosine Rule is:
c2 = atwo + b2 – 2ab cos (C)
Why Do I Need Trigonometry?
This is a reasonable question, and the respond is at to the lowest degree partly considering those who decide the mathematics curriculum in many countries recollect that yous should know about information technology, and for very skilful reason.
Trigonometry is said to be the most important mathematical relationship ever discovered. Triangles are ane of the virtually unproblematic forms constitute in nature, just their mathematics has vital importance, especially where precise distance measurements are needed. When we begin to think almost the applications where accurate distances are important, information technology is credible that there are dozens, including navigation in naval and aviation systems, astronomy, satellite systems, geographical surveys and cartography (maps), architecture and structural engineering, graphic design and computer generated imagery.
Many of these rely on a measurement technique known equally triangulation, which applies the concepts of trigonometry.
Example: Trigonometry and Navigation
When you lot are sailing or cruising at sea, where you lot end up is affected past:
- The direction in which you steer;
- The speed at which you travel in that management (i.e. the motor or wind speed); and
- The management and speed of the tide.
You lot can exist motoring in ane direction, but the tide could be coming from 1 side, and push you to the other. Y'all will demand trigonometry to piece of work out how far you will travel and in what precise management.

You will, quite rightly, have worked out that it'southward not quite as simple as all that, because the actual direction of travel depends on the tide speed and your speed, but you lot tin can probably see why trigonometry might be important!
Worked Example
You are out for a day's sailing, and don't really mind where you lot terminate upwards. Y'all started out heading due eastward, and program to sail for i hour at a cruising speed of x km/h. The tide is due n, and running at 5km/h. What direction volition you end upwardly travelling in?
-
First draw your triangle, and characterization the sides. You are heading due east, and so allow's brand that the bottom of the triangle, length 10km. The tide is going to push y'all north, so permit'south make that the right hand side. And you lot want to know what management you'll end upwards going in, then that's angle θ.

-
You have the reverse and the adjacent, which means that yous need to use tangent. Tan θ = Opposite/adjacent = 5/ten = 0.five.
-
Now is the fourth dimension to apply the inverse tan function. The inverse tan of 0.5 is 26.6°. In other words, tan 26.6 = 0.5.
-
Direction (your 'heading' in navigation) is measured from North, which is 0° on your compass. Your reply from (3), however, is measured from xc°, or East. You will therefore demand to subtract your respond from 90°, to obtain the reply: Yous are travelling in a direction (heading) of 63.4°, which is betwixt North E (45°) and East N Due east (67.5°).
Why is this important? Y'all'll demand to know which direction yous travelled in club to sail home, of course!
In real life, you will also need to remember that by then the tide may accept changed …
Conclusion
Trigonometry may not have all that many everyday applications, but it does help yous to work with triangles more than readily. It'due south a useful supplement to geometry and bodily measurements, and equally such well worth developing an understanding of the nuts, fifty-fifty if you never wish to progress further.
Source: https://www.skillsyouneed.com/num/trigonometry.html
0 Response to "Things You Need to Know About Trigonometry"
Post a Comment